La formule de Taylor Young est une technique mathématique permettant de développer une fonction sous forme d’une somme de termes polynomiaux.
I. Formule de Taylor Young
Cette méthode est très utilisée en analyse mathématique, notamment en calcul différentiel et en théorie de la probabilité.
Dans cet article, nous allons explorer les bases et ses différentes applications.
définition et bases théoriques
La formule de Taylor Young est une méthode permettant de développer une fonction en série de puissances.
Cette méthode permet de décrire localement une fonction à partir de sa valeur en un point et de ses dérivées à ce point.
Plus précisément, il permet de trouver une expression de la fonction en utilisant une série de termes polynomiaux centrés sur un point donné.
En mathématiques, la formule de Taylor Young s’écrit de la manière suivante :
f(x) = f(a) + f'(a)(x-a) + (f »(a)/2!)(x-a)^2 + … + (f^(n)(a)/n!)(x-a)^n + R_n(x)
où f(x) est la fonction à développer, f(a) est la valeur de la fonction en un point a,
f'(a) est sa dérivée première en a,
f »(a) est sa dérivée seconde en a, et ainsi de suite jusqu’à la n-ième dérivée de f en a, notée f^(n)(a).
Le terme R_n(x) représente le reste, c’est-à-dire la différence entre la fonction f(x) et sa forme développée de degré n.
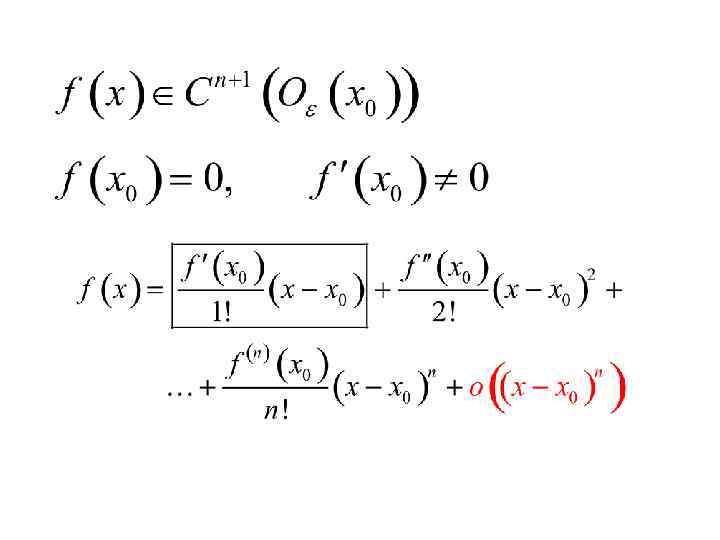
II. Exemples d’applications
La formule de Taylor Young peut être utilisée pour développer une fonction en série de puissances de manière exacte ou approchée.
Cette méthode est très utile en calcul numérique et en analyse mathématique, notamment pour trouver des approximations de fonctions complexes.
exemples d’applications
Voici quelques exemples d’applications de la formule de Taylor Young :
- Approximation de la fonction sinus : il permet de développer la fonction sinus en série de puissances, donnant la célèbre formule :
sin(x) = x – (x^3)/3! + (x^5)/5! – (x^7)/7! + …
En plus cette formule est très utile pour les calculs numériques impliquant des fonctions trigonométriques.
- Développement limité d’une fonction : il permet de trouver le développement limité d’une fonction en un point donné.
Par exemple, pour la fonction f(x) = ln(x) développée en x=1, on obtient :
ln(x) = (x-1) – ((x-1)^2)/2 + ((x-1)^3)/3 – …
- Calcul de dérivées : il peut être utilisée pour calculer les dérivées d’une fonction en un point donné.
Par exemple, pour la fonction f(x) = e^x, le développement de la formule de Taylor Young autour de x=0 donne :
e^x = 1 + x + (x^2)/2! + (x^3)/3! + …
Ainsi, ce qui permet de calculer la dérivée de la fonction en x=0, qui vaut 1.
formule de taylor young avec reste intégrale
La formule de Taylor-Young, également appelée formule avec reste intégrale.
Ainsi, c’est une formule mathématique qui permet d’approximer une fonction en utilisant sa valeur et ses dérivées en un point donné.
Elle est utilisée en analyse mathématique et en calcul numérique pour simplifier les calculs et obtenir des résultats précis.
La formule de Taylor-Young peut être écrite de la manière suivante :
f(x) = f(a) + f'(a)(x-a) + (1/2)f »(a)(x-a)^2 + … + (1/n!)f^(n)(a)(x-a)^n + Rn(x)
où f(a) est la valeur de la fonction en un point a,
f'(a) est sa dérivée première en ce point,
f »(a) est sa dérivée seconde, et ainsi de suite jusqu’à la dérivée n-ième f^(n)(a) en ce point.
Le terme Rn(x) est appelé reste intégrale, qui est une estimation de l’erreur commise en utilisant la formule de Taylor-Young pour approximer la fonction.
Le reste intégrale peut être exprimé de différentes manières, en fonction de la complexité de la fonction et du degré de précision souhaité.
Il peut être calculé en utilisant des formules d’intégration ou des inégalités comme le théorème de Taylor.
La formule est utilisée dans de nombreux domaines, tels que la physique, la finance, l’ingénierie, l’informatique, et bien d’autres.
En effet, elle permet d’approximer des fonctions complexes en utilisant des calculs simples, et elle est souvent utilisée pour résoudre des problèmes où la précision est importante.
En plus, un exemple d’utilisation de la formule de Taylor-Young serait dans le calcul de l’approximation d’une fonction trigonométrique telle que sin(x) ou cos(x).
Ainsi, en utilisant la formule avec un nombre suffisamment grand de termes, on peut obtenir une approximation très précise de la fonction pour des valeurs de x proches de zéro.
Finalement, cette approximation est souvent utilisée dans les calculs numériques, la simulation de systèmes dynamiques, ou encore pour le calcul de dérivées et d’intégrales.
